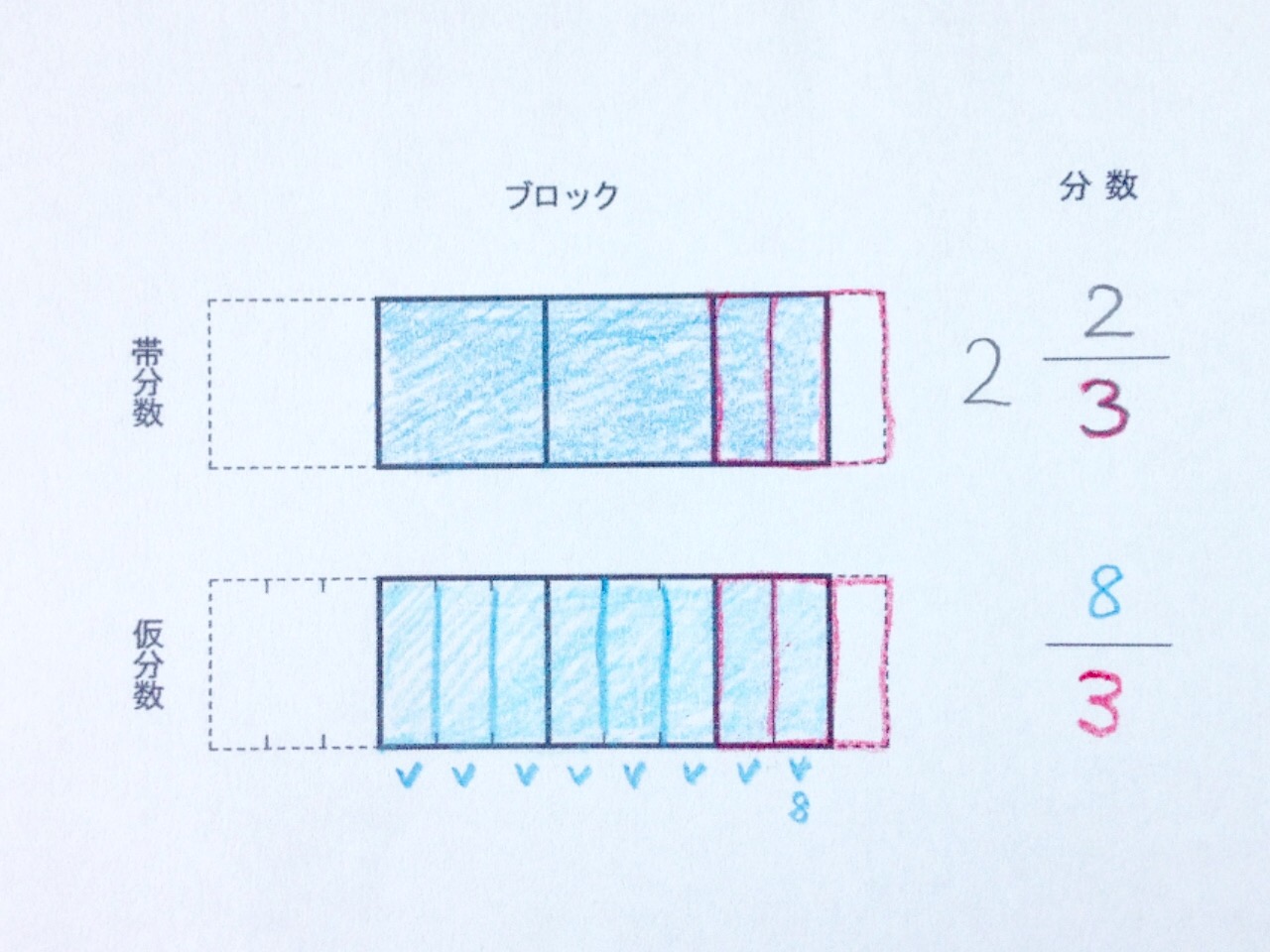
帯分数と仮分数の量イメージが不足しているため、分数の四則のイメージ理解ができない児童がいます。そこで今回、ブロック図と色鉛筆をつかって、「帯分数と仮分数」表現の違いを学ぶワーク指導をご紹介します。
仮分数の量イメージがつかめない原因
分数の四則計算をしっかり理解する上で、帯分数と仮分数のイメージ理解は避けられません。特に仮分数の量イメージについては、不足している児童が大勢います。その主な原因は、以下のとおりです。
- 仮分数がでる場面では、手続きばかり重視され量イメージを想起する機会がない
この解決の方法として、以下を目的とするプリントワークを設けました。
- 色鉛筆を使って量イメージから帯分数と仮分数のイメージ解釈する
- 帯分数・仮分数のイメージ解釈から分数で表現する。
このプリントワークの指導方法をご紹介します。
量イメージから帯分数・仮分数を表現するワーク
帯分数と仮分数を、量イメージのブロックと分数欄があります。
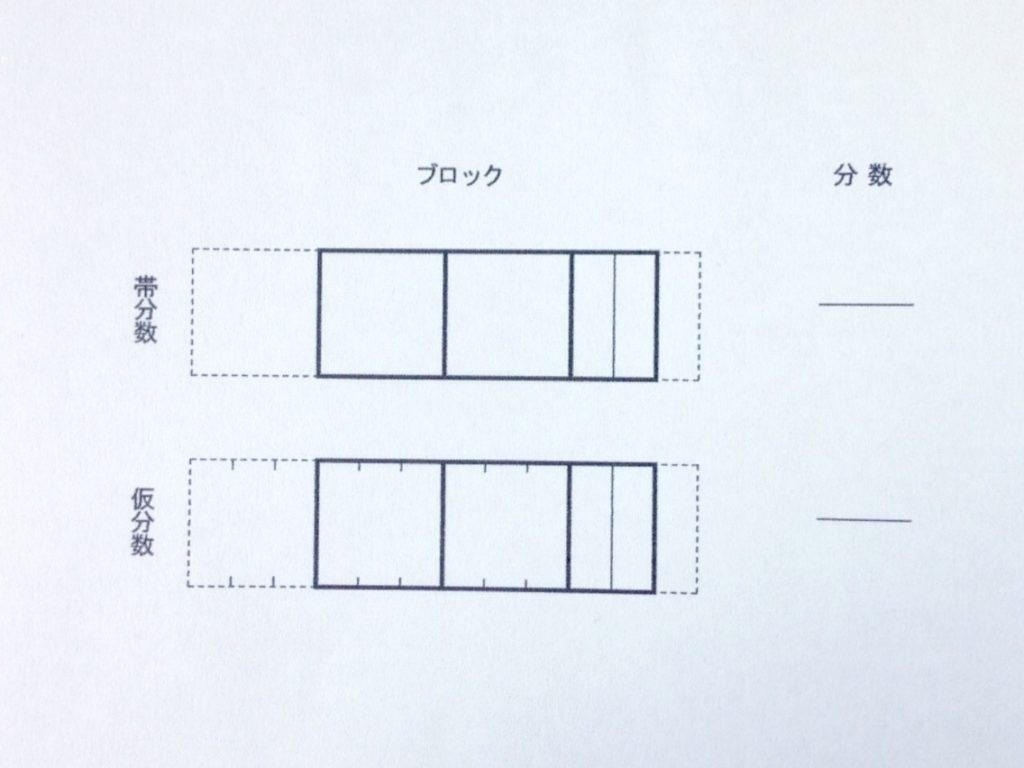
帯分数と仮分数の量イメージのブロックに、色鉛筆で分数のイメージ解釈をします。そしてそれぞれ分数表記へと移ります。まずは、帯分数から始めます。
帯分数の分割枠(分母の数)を描く
赤い色鉛筆で分数部分にあたる「分割枠」を描きます。
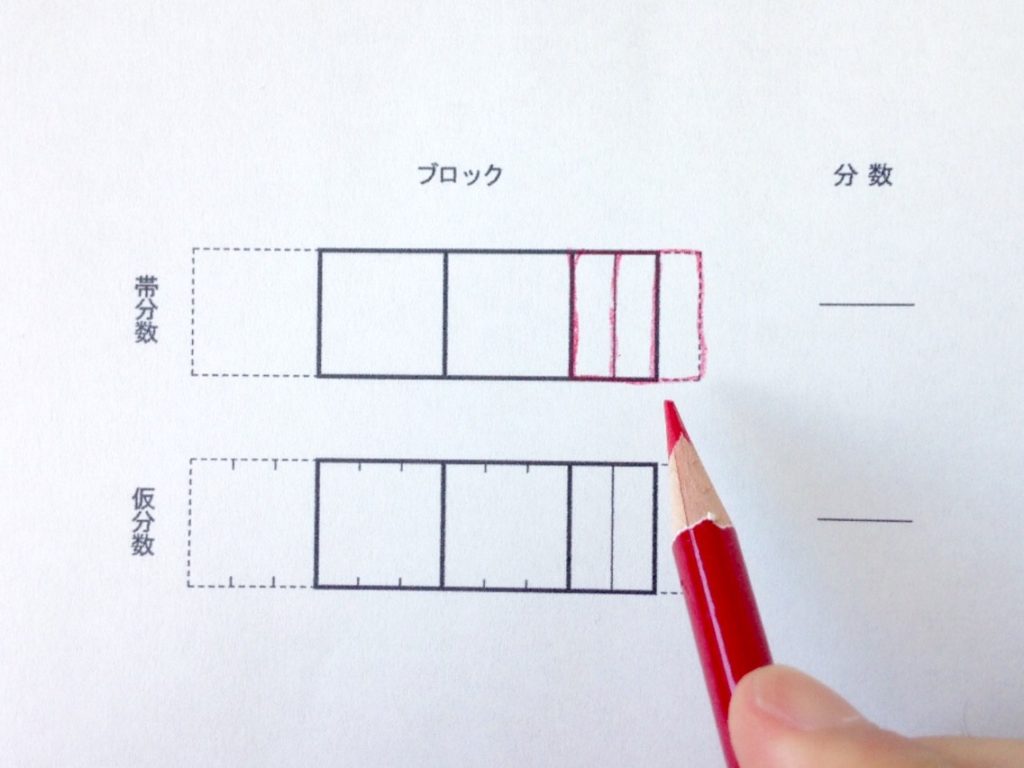
赤い分数枠は、正方形のブロックの中に3つ入ることが分かります。
帯分数の量イメージを描く
青の色鉛筆でブロックを丁寧に塗ります。
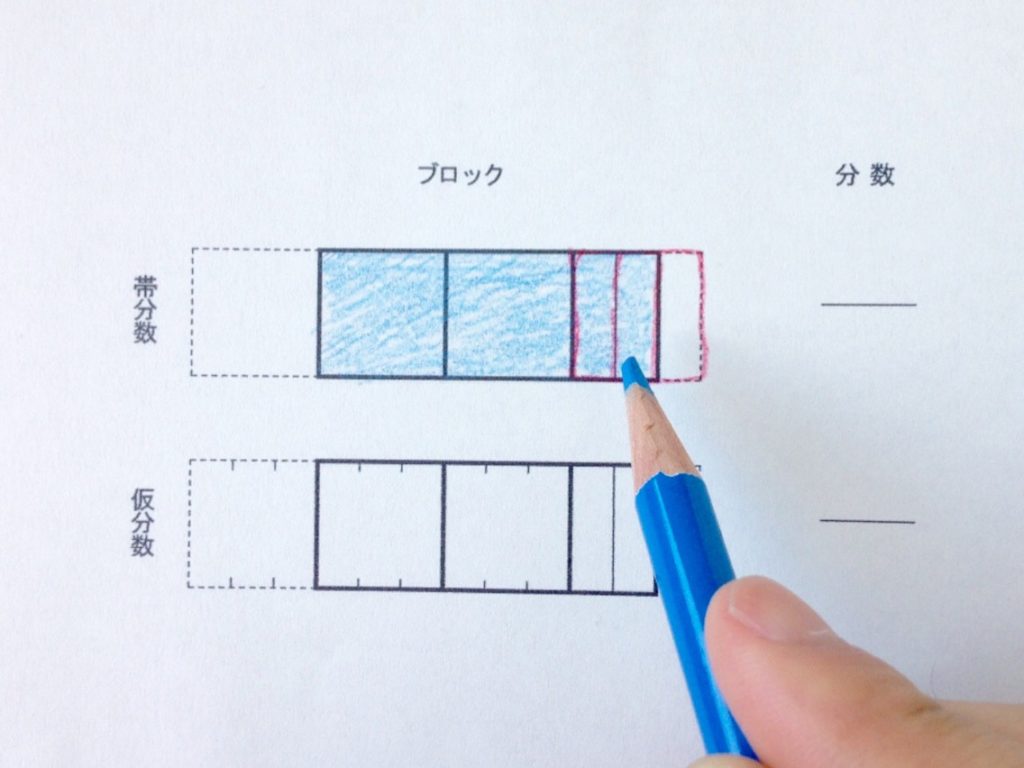
これで整数部分にあたる正方形ブロックが2つ、小数部分にあたる分割ブロックが2つとハッキリ分かります。
帯分数で表記する
ブロックをみて、分数で書いてみます。
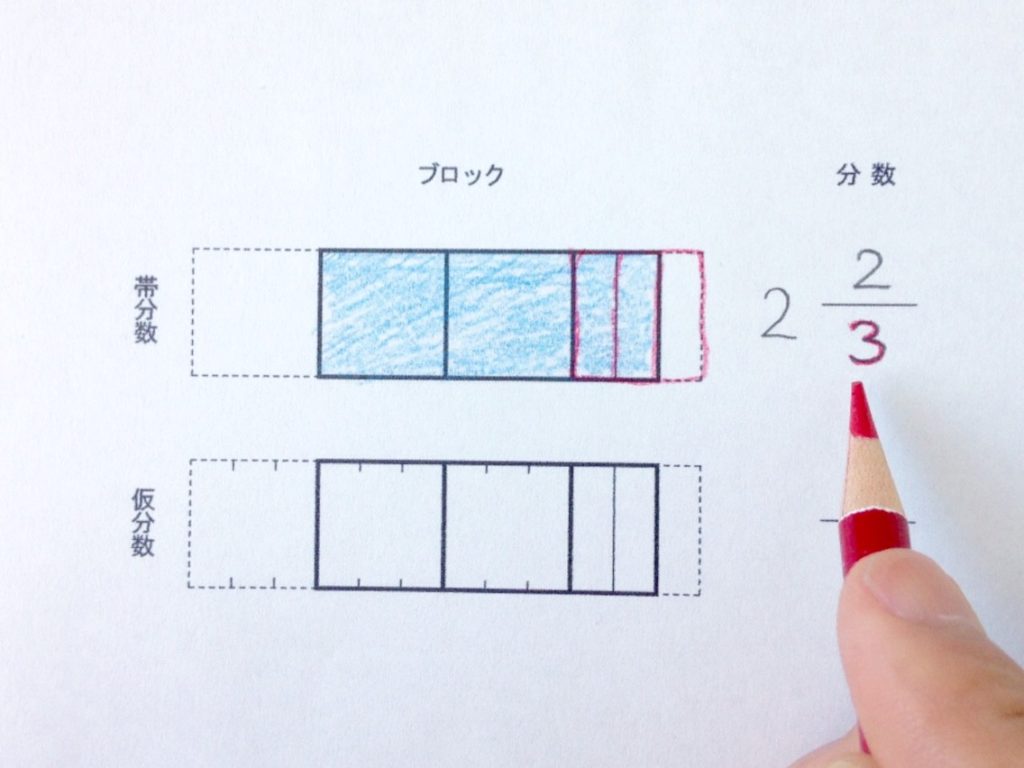
整数部分の正方形ブロック(青色)は2つ、これは分数の整数部分。分割枠(赤色)の数3は分母の数にあたります。分割ブロック(青色)は2つ、これは分子にあたります。
仮分数の分割枠(分母の数)を描く
帯分数と同じように、赤い色鉛筆で分数部分にあたる「分割枠」を描きます。
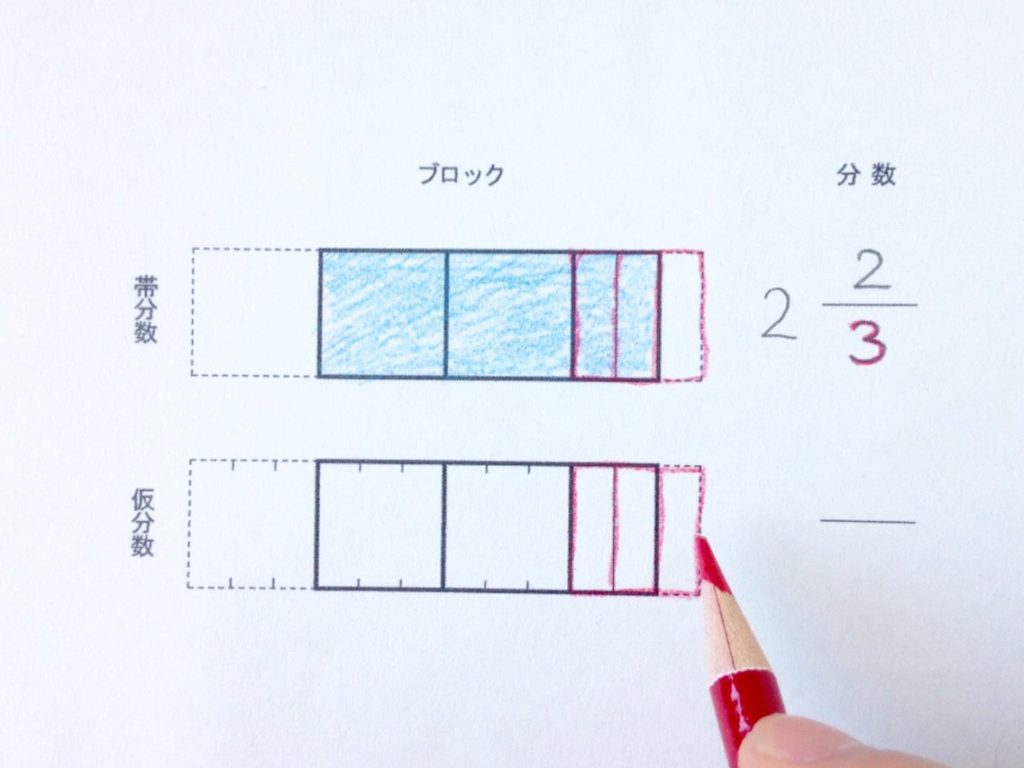
仮分数の量イメージを描く
次も帯分数と同じように、青の色鉛筆でブロックを塗ります。
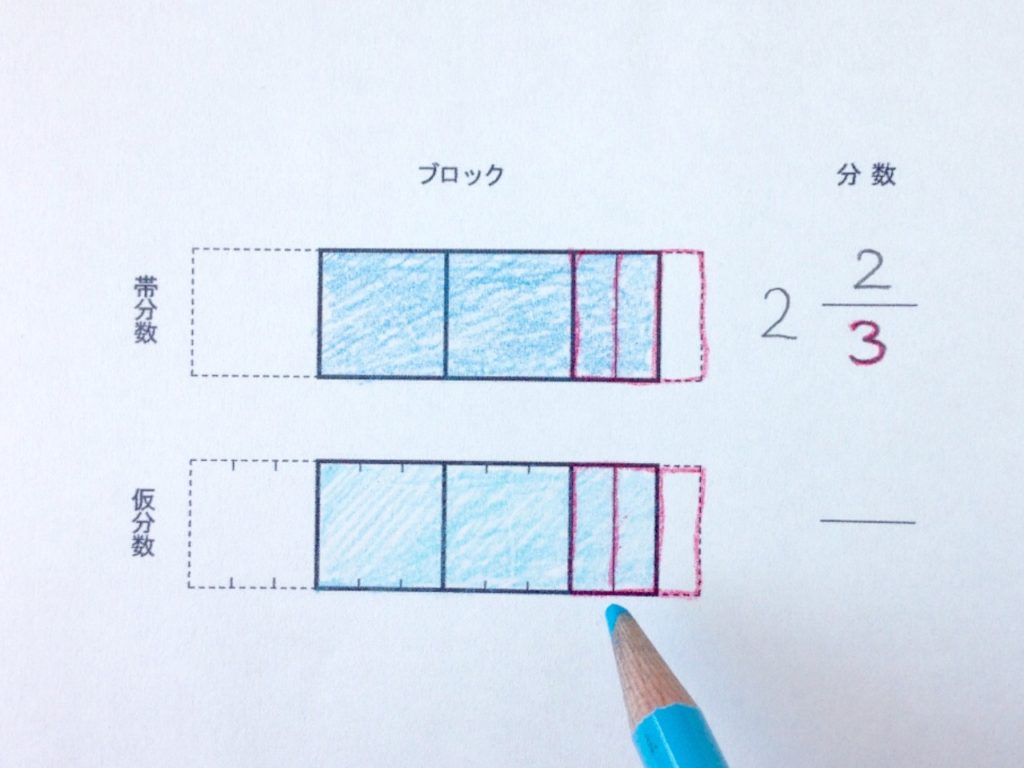
ここまで帯分数と同じです。ここから仮分数はもうひとつ作業が入ります。できれば濃いめの青の色鉛筆に持ちかえます。
仮分数は、整数ブロックをすべて分数ブロックに変えたものです。そこで分数枠と同じ大きさで、整数ブロックに切れ目を入れます。
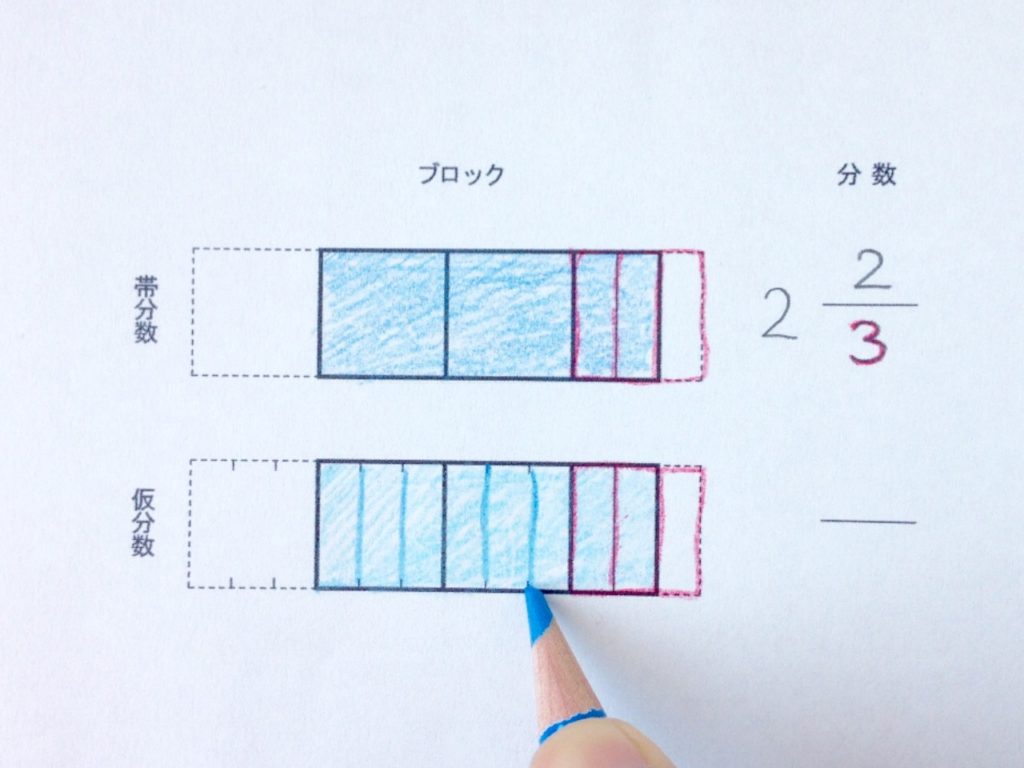
切れ目を入れたことで、全てが分数ブロックになりました。ここで今一度、分数ブロックの個数をかぞえます。
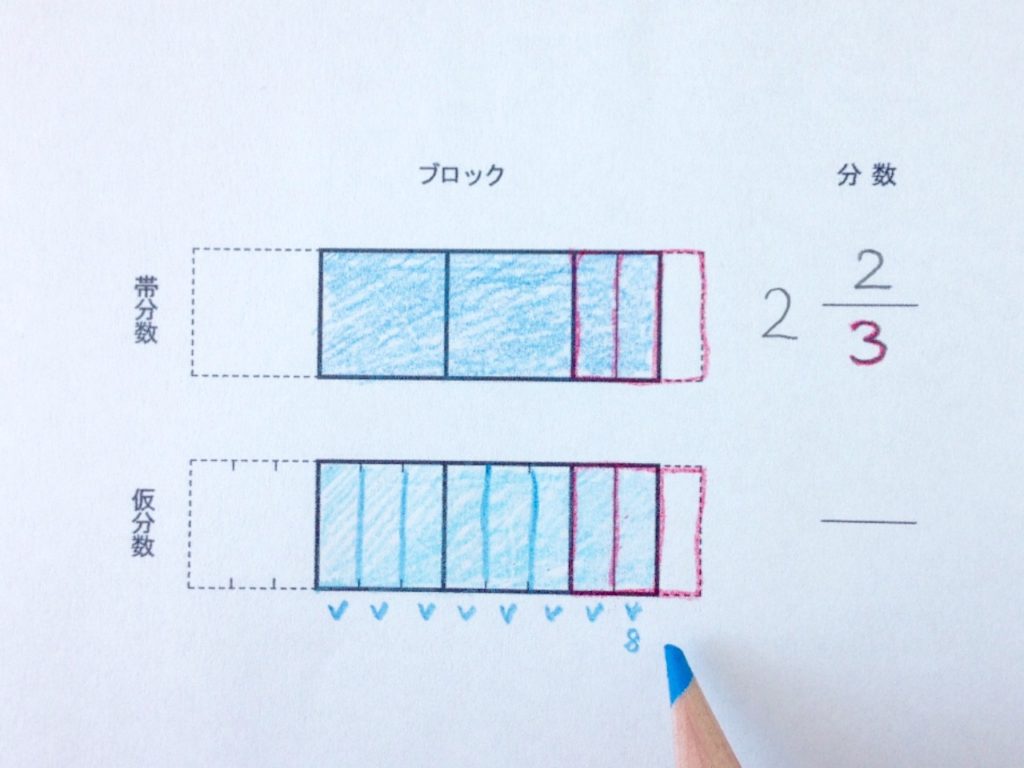
仮分数の分数ブロックは8個ありました。小さく記入しておきましょう。
仮分数で表記する
仮分数のブロックをみて、分数で表します。
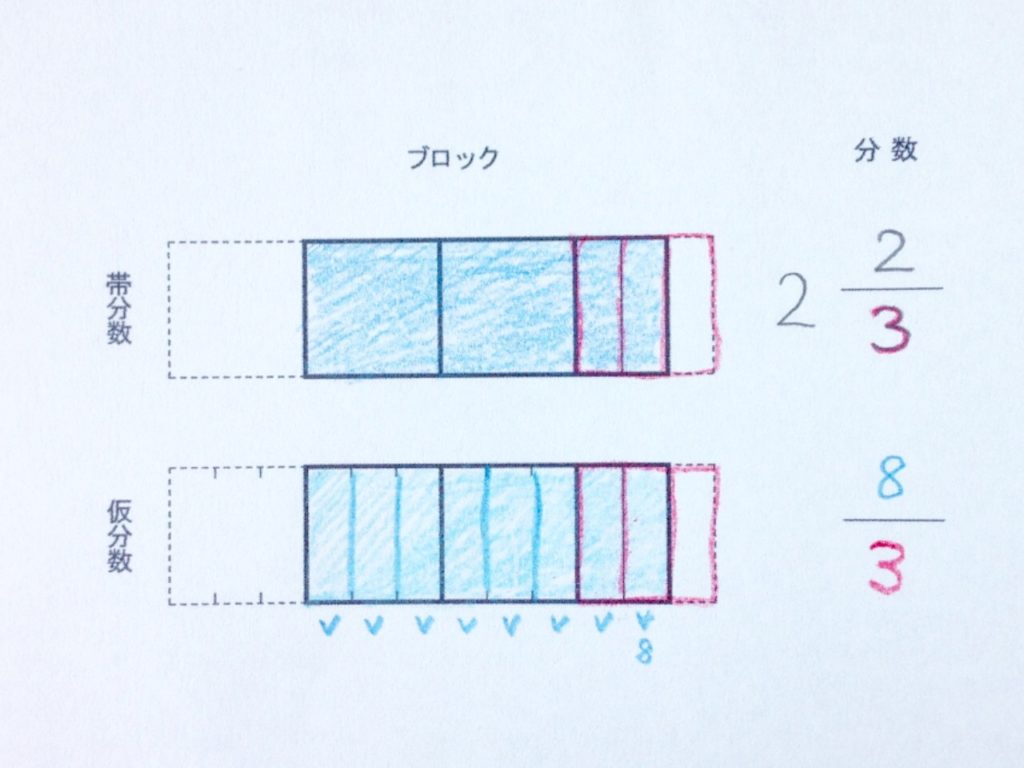
整数ブロックはなくなり分数ブロック(青色)が8つ。分数枠(赤色)は3つ。それで分数で表現します。
最後に
量イメージを帯分数と仮分数で表現することで、分数のたし算の繰り上り・ひき算の繰り下がりが理解できます。また、かけ算において、仮分数に直して計算する理由もこのイメージから分かります。
算数が不得意な児童は、手続き習得ばかりが目的化され、根底にある「数の理解」が疎かになりがちです。ぜひ、一度は「量イメージ」から「分数表記」へかえるワークに取組んで欲しいと思います。